Celebrating π Day ….
William Jones 1674-1749 was the mathematician who coined the symbol π. Born in Anglesey, he introduced the sign π to represent the ratio between the circumference of a circle and its diameter. For more information on Welsh Mathematicians please visit: Welsh Mathematicians
Archimedes & π
See how Archimedes calculated π … play with this geogebra app here.
Best viewed full screen
To access all of the Geogebra apps created by FMSPW please go to our resources page and for Geogebra professional learning head to here. Please ask if there is something you’d like but you can’t see it.
Locating π
Find your birthday / phonenumber / lucky number in π ….. https://www.atractor.pt/mat/fromPI/Pisearch-_en.html

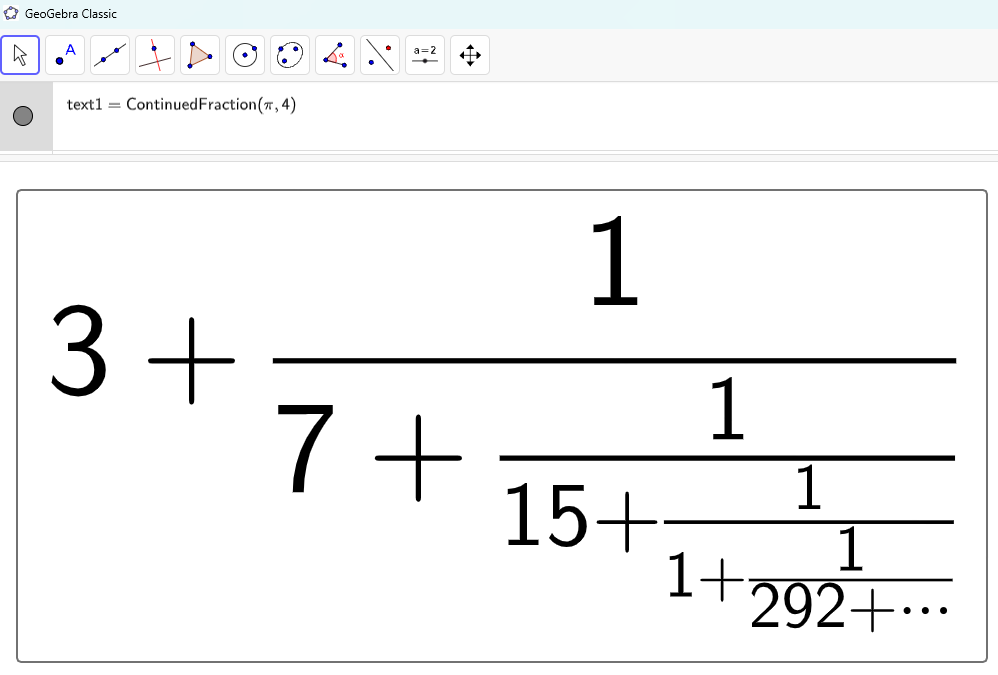
Continued Fractions, π & Geogebra
Did you know you can get continued fractions on Geogebra…?
π jokes (sorry they are bad!)
Did you know?
That 3.14% of sailors are Pi-rates!
Why did pi fail its driving test?
Because it didn’t know when to stop.
What do you call it when someone gets a huge tattoo of pi on their face?
An irrational decision.
What did pi say to its sweetheart?
You look radian today.
What do you get when a bunch of sheep stand around in a circle?
Shepherd’s pi.
What is a mathematician’s favourite snake?
A pi-thon.
What did the triangle feel sorry for the circle?
Because it’s pointless.
π poems!
In this poem the length of the words tell you the value of the next digit in π. Can you write your own? Share it with us @RhGMBC_FMSPW
Now I, even I, would celebrate
In rhymes unapt the great
Immortal Syracusan, rivaled nevermore,
Who in his wond’rous lore,
Passed on before,
Left men his guidance
How to circles mensurate.
π Competition

Challenge your students to represent π in any interesting way that they choose. For example, they could do some artwork, make a piece of music or write a poem. Or they might think of something we’ve not thought of! Think Maths will post a small π -related prize to their three favourite entries, and will tweet and feature on the website their 10 favourite entries. The deadline for entry is Friday March 31st 2023.
See their website for more details and for instructions on how to enter: https://think-maths.co.uk/pi-project
Numberphile discuss π
Some history on π
Pi is the ratio of a circle’s circumference to its diameter i.e.
![]()
The value of π (pi) has been known for almost 4000 years. [If we calculated the number of seconds in 4000 years and worked out the value of π to that number of decimal places, it would still only be an approximation for the actual value of π.]
One Babylonian tablet (ca 1900-1680 BCE) has a value π = 3.125.
The “Rhind Papyrus” (ca 1650 BCE) gives an insight to Egyptian Mathematics and they came up with a value of π = 3.1605.
The first calculation of π was completed by Archimedes of Syracuse (287-212 BCE). His method came up with a value that π was somewhere between ![]() and
and ![]() . The value of
. The value of ![]() was commonly used in schools before calculators were in widespread use. (It explains why the radius and diameter of circles were always given as multiples of 7.)
was commonly used in schools before calculators were in widespread use. (It explains why the radius and diameter of circles were always given as multiples of 7.)
Zu Chongzhi (429-501) from China, calculated the value as ![]() (not very nice to work with so it didn’t catch on).
(not very nice to work with so it didn’t catch on).
The symbol that we use to represent π was introduced by the Welshman William Jones (Ynys Mon, 1675-1749) in 1706. Initially, it was not popular.
The symbol was popularized by Leonhard Euler (Swiss, 1707-1783) who adopted it in 1737.
In the eighteenth-century, a French mathematician named Georges Buffon (1707-1788) devised a way to calculate π based on probability (see Buffon’s needle).
Π is defined as an irrational number which means that you cannot write it as an exact fraction (top heavy in this case). This means that it is an infinite non-recurring decimal number.
How many digits do we need for calculations?
In school we tend to work with 3 digits most of the time (3.14).
NASA only uses 15 digits for π in its calculations for sending rockets into space. (See the film “Hidden Figures” about the life of Katherine Johnson.)
To measure the universe to an accuracy that is less than the size of an atom you would only need to use the first 40 digits of π.
These last three points does make you ask why we bother to investigate the accuracy of π any further.
Teacher Resources on Line (cleavebooks.co.uk)
Some notable dates in the development of π are in the table below.
| Date | Digits | Comment |
| ≈2000 BCE | 4 | Babylonian |
| ≈800 BCE | 7 | |
| 480 CE | 8 | |
| 1400 | 10 | |
| 1596 | 20 | |
| 1706 | 100 | Symbol introduced |
| 1853 | 261 | |
| 1853 | 440 | |
| 1946 | 620 | Most by hand |
| Jan 1947 | 710 | First by desk calculator |
| 1949 | 1120 | Last by desk calculator |
| 1949 | 2037 | First by computer – 70 hours |
| Jan 1958 | 10,000 | 1.7 hours |
| 1961 | 100,265 | 8.7 hours |
| 1967 | 500,000 | 28 hours |
| 1973 | 1,001,250 | 23.3 hours |
| 1981 | 2,000,036 | |
| Jan 1987 | 134,214,700 | |
| Aug 1989 | 1,011,196,691 | First to a billion |
| 29th Apr 2009 | 2,576,980,377,524 | 29.09 hours |
| 28th Dec 2013 | 12,100,000,000,050 | 94 days |
| 14th Aug 2021 | 62,831,853,071,796 | 108 days |

 Maths Support Programme Wales
Maths Support Programme Wales